题解Week3(2)

题解Week3(2)

四月 14, 2022

7-4

人类正在经历一场生化危机，许多城市已经被病毒侵袭，这些城市中的人们为了避免感染病毒，计划开车逃往其他没有被病毒入侵的城市（安全城市）。有些城市之间有公路直达，有些没有。虽然他们知道哪些城市是安全的，但是不知道有没有一条安全路径能够到达安全城市（只有该路径上经过的所有城市都是安全的，该路径才是安全路径）。请你编写一个程序帮助他们判断。

这还是我在没接触过搜索算法的时候写的

这道题我用的是递归写的。

看代码的中午注释（有些英文注释纯属debug发病）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <iostream>
#include <vector>
using namespace std;
vector<int> city[100];//描述每个城市的通路
int flag=0,startcity,endcity;
int Gone[100],safe[100];
void Find(int n){//寻找第N个城市是否有路可通。
//	cout << "Here is " << n << endl;
    Gone[n]=1;//这个城市已经走过了。
     if(n==endcity){flag=1;return;}//抵达城市
    else if(city[n].empty()==true){return;}//抵达死路（这句话好像没用的样子）
    else{
        for(int i=0;i<city[n].size();i++){
//        		printf("Here is city %d , and I am going to city %d . \n",n,i);
           		if(Gone[city[n][i]]!=1) Find(city[n][i]);//遍历下一条路
        }
    }
}
int main(){
    int n,m,k;
    cin >> n >> m >> k;
    int safecitynu;
    int r1,r2;

    for(int abc=1;abc<=m;abc++){
        cin >> safecitynu;
        safe[safecitynu]=1;
    }
    for(int abc=1;abc<=k;abc++){
        cin >> r1 >> r2;
        city[r1].push_back(r2);
        city[r2].push_back(r1);
    }
/*    for(int i=0;i<5;i++){
    	printf("city %d has %d\n",i,city[i].size());
    	for(int j=0;j<city[i].size();j++) printf("     city %d connect city %d\n",i,city[i][j]);
	}*/
    cin >> startcity >> endcity;
    if(safe[endcity]==0){printf("The city %d is not safe!",endcity);return 0;}
    else{
        Find(startcity);
        if(flag==1) printf("The city %d can arrive safely!",endcity);
        else printf("The city %d can not arrive safely!",endcity);
    }
    return 0;
}

7-2

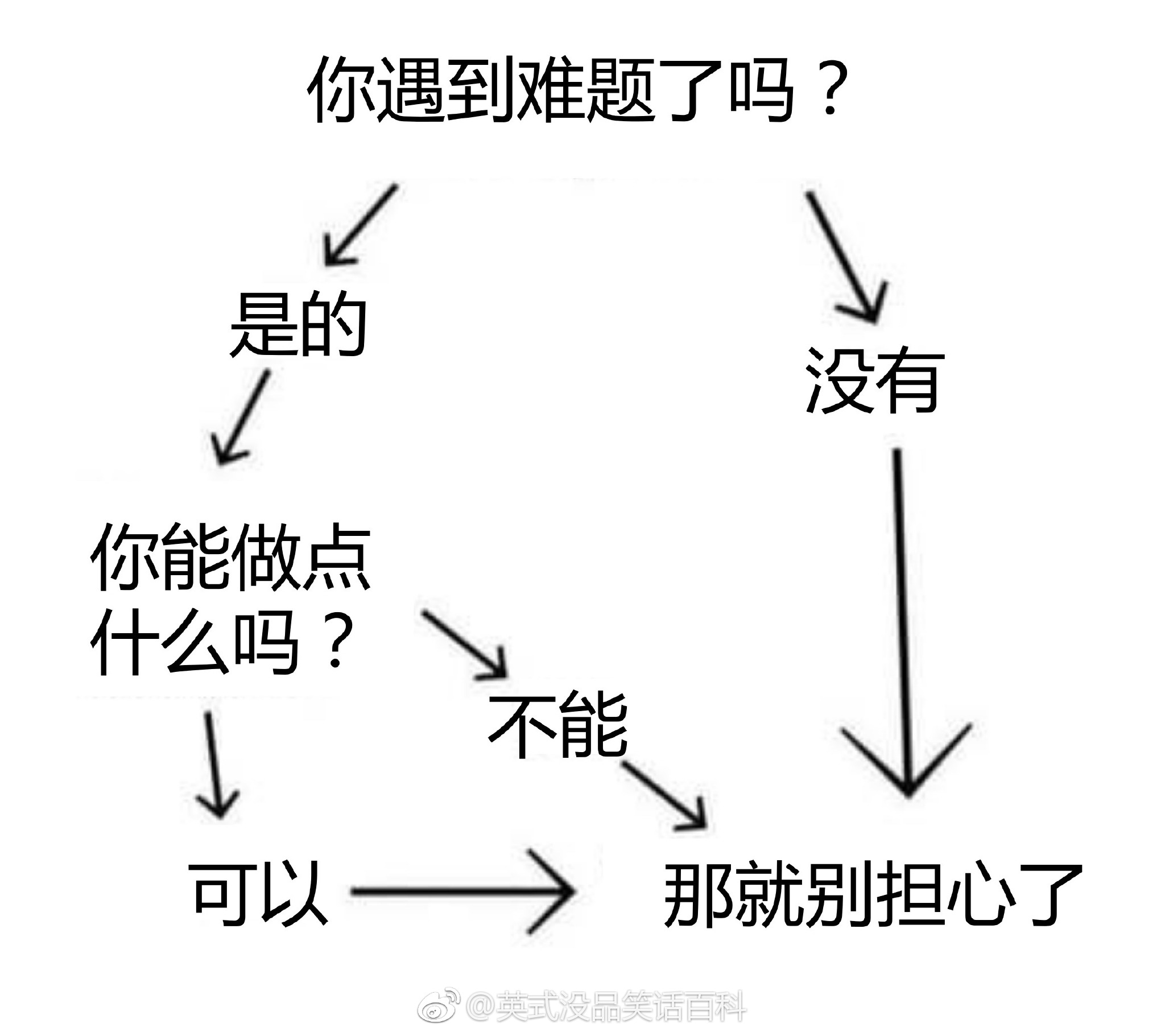
下图转自“英式没品笑话百科”的新浪微博 —— 所以无论有没有遇到难题，其实都不用担心。

ziqia.jpg

博主将这种逻辑推演称为“逻辑自洽”，即从某个命题出发的所有推理路径都会将结论引导到同一个最终命题（开玩笑的，千万别以为这是真正的逻辑自洽的定义……）。现给定一个更为复杂的逻辑推理图，本题就请你检查从一个给定命题到另一个命题的推理是否是“逻辑自洽”的，以及存在多少种不同的推理路径。例如上图，从“你遇到难题了吗？”到“那就别担心了”就是一种“逻辑自洽”的推理，一共有 3 条不同的推理路径。

本题实在我学习dfs的时候写的。

学习的地方在这——>柳萌的博客

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <vector>
using namespace std;
vector<int> pro_bridge[505];//每个逻辑的连线，和之前那道题一样
int reasonway[505];//这是储存抵达目标命题的路
int flag=1;//存在有其他的死路
int reasoning(int now){
	if(reasonway[now]==0){//抵达命题的通路这个值是默认为0,而目标点的reasonway是1
		for(int i=0;i<pro_bridge[now].size();i++){
			int next=pro_bridge[now][i];//遍历
			if(reasonway[next]==0) reasoning(next);//堆栈
			reasonway[now]+=reasonway[next];//储存树的节点数
		}
		if(reasonway[now]==0) flag=0;
	}
	return reasonway[now];
}
int main(){
	int n,m;
	cin >> n >> m;
	int logic1,logic2;
	for(int abs=1;abs<=m;abs++){
		cin >> logic1 >> logic2;
		pro_bridge[logic1].push_back(logic2);
	}
	int A,B;
	cin >> A >> B;
	reasonway[B]=1;
	reasoning(A);
	if(flag==1) cout << reasonway[A] << " Yes" << endl;
	else cout << reasonway[A] << " No" << endl;
	return 0;
}

7-3

扫雷是一款经典游戏，也是Windows操作系统最早引入的一款游戏，其最为经典的版本是Windows XP操作系统自带的扫雷游戏，曾风靡一个时代，是一代人的永恒记忆。

minegame.jpg

简单来说，其游戏界面由n行m列方格组成，其中k个方格后面隐藏着地雷。当用户点击一个方格时：

（1）如果该方格后面隐藏着地雷，则游戏结束，用户失败。

（2）如果该方格不是地雷，则该方格被打开：

  • 若该方格与地雷相邻（即该方格上、下、左、右、左上、左下、右上、右下相邻的8个方格内有地雷），则该方格处显示一个数字，表示其周围8个方格中的地雷数。
  • 若该方格未与地雷相邻（即该方格周围8个格子内没有地雷），则该方格的未被打开的邻居（即与该方格上、下、左、右、左上、左下、右上、右下相邻的方格）、邻居的邻居、邻居的邻居的邻居……都会被逐级打开，直到某方格与地雷相邻。这期间每个方格的处理方式同（2）。

（3）当所有没隐藏地雷的方格均被打开（即所有没打开的方格后都有地雷），则游戏结束，用户获胜。

请编写程序从初始界面开始，对于一系列用户的点击，求出点击之后的游戏界面。未打开的方格用-1表示，即游戏初始时为n行m列-1。已打开且未与雷相邻的方格用0表示，已打开且与雷相邻的方格用数字a (1≤ a ≤ 8)表示，即与之相邻的地雷数。

a?

本题踩坑，打开打开的地方的判断时，我判断它这个点等于0了，实际上应该是不等于-1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <iostream>
using namespace std;
int a[26][26],boom[26][26],opened[26][26];
int dx[8]={1,1,0,-1,-1,-1,0,1};//方向dfs
int dy[8]={0,-1,-1,-1,0,1,1,1};
int boomnum=0;
bool losethegame=false;
bool testthewinstage(){//因为数组较小，遍历每一个点来测试是不是赢了。
	for(int i=0;i<=21;i++){
		for(int j=0;j<=21;j++){
			if(a[i][j]==-1&&boom[i][j]!=1) return false;
		}
	}
	return true;
}
void Open(int x,int y){//打开这个点。
	if(a[x][y]==-1){
		if(boom[x][y]==1) {losethegame=true;return;}
		int nextx,nexty;
		boomnum=0;
		for(int aaa=0;aaa<8;aaa++){
			nextx=x+dx[aaa];//遍历四周
			nexty=y+dy[aaa];
			if(nextx>=0&&nextx<=20&&nexty>=0&&nexty<=20){
				if(a[nextx][nexty]==-1&&boom[nextx][nexty]==1){
					boomnum++;
				}
			}
		}
		a[x][y]=boomnum;
		if(boomnum==0){//如果没有点，则遍历四周
			for(int k=0;k<8;k++){
				nextx=x+dx[k];
				nexty=y+dy[k];
				if(nextx>=0&&nextx<=20&&nexty>=0&&nexty<=20){
				if(a[nextx][nexty]==-1&&boom[nextx][nexty]==0){
					Open(nextx,nexty);
				}
			}

			}
		}
		return;
	}
}
int main(){
	int n,m,k,l;
	cin >> n >> m >> k >> l;
	for(int i=0;i<=25;i++) for(int j=0;j<=25;j++) a[i][j]=-2;
	for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) a[i][j]=-1;
	int i,j;
	for(int abc=1;abc<=k;abc++){
		cin >> i >> j;
		i++;
		j++;
		boom[i][j]=1;
	}
	for(int abc=1;abc<=l;abc++){
		cin >> i >> j;
		i++;
		j++;
        if(a[i][j]!=-1) continue;//踩坑点
		Open(i,j);
		if(losethegame==true) {cout << "You lose";break;}
        for(int i=1;i<=n;i++){
			for(int j=1;j<=m;j++) cout <<a[i][j]<< " ";
			cout << endl;
		}
		if(testthewinstage()==true) {cout << "You win";}//注意格式昂
		cout << endl;
	}
	return 0;
}

7-4

有一个仅由数字0与1组成的n*n格迷宫。若你位于一格0上，那么你可以移动到相邻4格中的某一格1上，同样若你位于一格1上，那么你可以移动到相邻4格中的某一格0上。
你的任务是：对于给定的迷宫，询问从某一格开始能移动到多少个格子（包含自身）。

疯狂踩坑

搜索好难啊QAQ

下面是一个超时的解答，因为是很普通的bfs，果断超时。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <queue>
using namespace std;
int dx[4]={1,0,-1,0};
int dy[4]={0,-1,0,1};
int m[1005][1005];
int vis[1005][1005];
struct point{
	int x;
	int y;
	int step;
};
queue<point> road;
int main(){
	int n,mm;
	cin >> n >> mm;
	char chnu;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			cin >> chnu;
			m[i][j]=chnu-'0';
		}
	}
	int startx,starty,nexty,nextx;
	for(long long abc=1;abc<=mm;abc++){
		int ans=1,sum=1;
		cin >> startx >> starty;
		for(int i=0;i<=n;i++) for(int j=0;j<=n;j++) vis[i][j]=0;
		point start,next;
		start.x=startx;
		start.y=starty;
		sum=1;
		vis[startx][starty]=1;
		road.push(start);
		while(!road.empty()){
			start=road.front();
			for(int k=0;k<4;k++){
				next.x=start.x+dx[k];
				next.y=start.y+dy[k];
				if(next.x<=n&&next.y<=n&&next.x>0&&next.y>0&&m[next.x][next.y]!=m[start.x][start.y]&&vis[next.x][next.y]==0){
				//	printf("Here I got %d %d\n",next.x,next.y);
					vis[next.x][next.y]=1;
					road.push(next);
					sum++;
					ans=max(ans,sum);
				}
			}
			road.pop();
		}
		cout << ans << endl;
	}
	return 0;
}

经考虑和被m的大小吓到了，我采用了初始化的一种方案，先把每个点的值都找到，有了m就直接输出。

但是还是超时。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <iostream>
#include <queue>
using namespace std;
int dx[4]={1,0,-1,0};
int dy[4]={0,-1,0,1};
int m[1005][1005];
int vis[1005][1005];
int memo[1005][1005];
int blockarea[1000005];
struct point{
	int x;
	int y;
};
queue<point> road;
int main(){
	int n,mm;
	cin >> n >> mm;
	char chnu;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			cin >> chnu;
			m[i][j]=chnu-'0';
		}
	}
	int block=0;
	int nexty,nextx,startx,starty;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(memo[i][j]==0){
				block++;
				int sum=1;
				int flag=0;
			//	cin >> startx >> starty;
				for(int i=0;i<=n;i++) for(int j=0;j<=n;j++) vis[i][j]=0;
				point start,next;
				start.x=i;
				start.y=j;
				vis[i][j]=1;
				road.push(start);
				memo[i][j]=block;
				while(!road.empty()){
					start=road.front();
					for(int k=0;k<4;k++){
						next.x=start.x+dx[k];
						next.y=start.y+dy[k];
						if(next.x<=n&&next.y<=n&&next.x>0&&next.y>0&&m[next.x][next.y]!=m[start.x][start.y]&&vis[next.x][next.y]==0){
						//	printf("Here I got %d %d\n",next.x,next.y);
							vis[next.x][next.y]=1;
							road.push(next);
							memo[next.x][next.y]=block;
							sum++;
						}
					}
					road.pop();
				}
			//	cout << ans << endl;
				blockarea[block]=sum;
			}
		}
	}
	for(int abs=1;abs<=mm;abs++){
		cin >> startx >> starty;
		cout << blockarea[memo[startx][starty]] << endl;
	}
	return 0;
}

最后我学习了一下联通块，

在一次遍历中，易证一次遍历中每个点的结果是一样的，

于是就可以把一次遍历的结果保存到block这个数组中。

几个超时小技巧：

1、开超大数组

2、每次都清一次数组（vis[i][j]=0;)

注意别踩了，debug一天了都。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <iostream>
#include <queue>
using namespace std;
int dx[4]={1,0,-1,0};
int dy[4]={0,-1,0,1};
int m[1005][1005];
int memo[1005][1005];
int blockarea[1000005];
struct point{
	int x;
	int y;
};
queue<point> road;
int main(){
	int n,mm;
	cin >> n >> mm;
	char chnu;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			cin >> chnu;
			m[i][j]=chnu-'0';
		}
	}
	int block=0;
	int nexty,nextx,startx,starty;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(memo[i][j]==0){
				block++;
				int sum=1;
				int flag=0;
			//	cin >> startx >> starty;
				point start,next;
				start.x=i;
				start.y=j;
				road.push(start);
				memo[i][j]=block;
				while(!road.empty()){
					start=road.front();
					for(int k=0;k<4;k++){
						next.x=start.x+dx[k];
						next.y=start.y+dy[k];
						if(next.x<=n&&next.y<=n&&next.x>0&&next.y>0&&m[next.x][next.y]!=m[start.x][start.y]&&memo[next.x][next.y]==0){
						//	printf("Here I got %d %d\n",next.x,next.y);
							road.push(next);
							memo[next.x][next.y]=block;
							sum++;
						}
					}
					road.pop();
				}
			//	cout << ans << endl;
				blockarea[block]=sum;
			}
		}
	}
	for(int abs=1;abs<=mm;abs++){
		cin >> startx >> starty;
		cout << blockarea[memo[startx][starty]] << endl;
	}
	return 0;
}
  1. 1. 7-4
  2. 2. 7-2
  3. 3. 7-3
  4. 4. 7-4